การคำนวณทางด้านกลศาสตร์โครงสร้าง (STRUCTURAL MECHANICS COMPUTATION หรือ SMC)
หัวข้อในวันนี้จะเกี่ยวข้องกันกับหัวข้อ การคำนวณทางด้านกลศาสตร์โครงสร้าง (STRUCTURAL MECHANICS COMPUTATION หรือ SMC) นะครับ
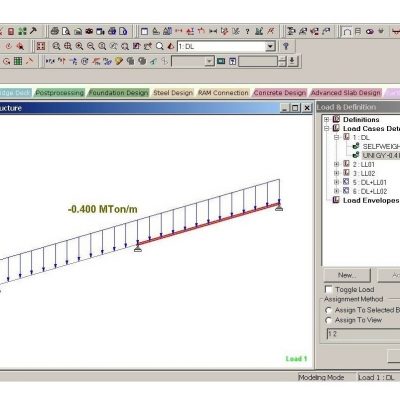
วันนี้ผมจะขออนุญาตมาทำการยก ตัวอย่าง พร้อมกับอธิบายหลักในการวิเคราะห์โครงสร้างคานรับแรงดัดที่ต้องรับแรงกระทำชนิดแผ่กระจายตัวแบบสม่ำเสมอ (DISTRIBUTED LOAD) ในรูปแบบที่มีความแตกต่างกันทั้ง 3 รูปแบบนี้ให้แก่เพื่อนๆ ทุกคนได้รับทราบกันต่อจากโพสต์ของเมื่อ 2 วันก่อนหน้านี้ โดยที่ในวันนี้จะเป็นคานรูปแบบสุดท้ายนะครับ
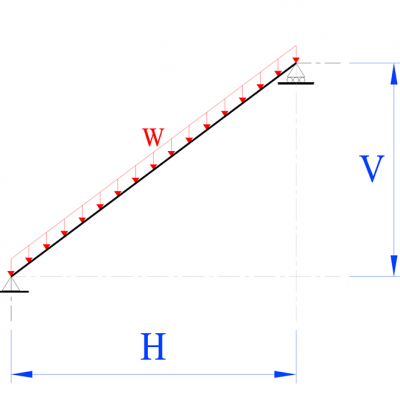
วันนี้เราจะมาต่อกันที่คานในรูปขวามือสุดกันนะครับ ในรูปแบบๆ นี้จะเป็น นน ที่เกิดขึ้นใน แนวระนาบที่คานมีการเอียงตัว และ เกิดจากการถ่าย นน มาลงบนโครงสร้างคานรับแรงดัดโดยตรงนั่นเองนะครับ เช่น นน ของโครงสร้างส่วนอื่น หรือ นน ของงานระบบอื่น ที่ถ่าย นน มาลงยังคานชุดนี้โดยตรง เป็นต้นครับ
ก่อนการวิเคราะห์โครงสร้างเราจะสามารถทำการตรวจสอบได้ว่าคานชนิดนี้มีค่า PARAMETER ที่เราทราบค่าอยู่ทั้งหมด 3 ค่า คือ
EQ.EQ. (EQUILOIBRIUM EQUATION) = 3 EQUATIONS
C (INTERNAL HINGES) = 0 Nos.
ดังนั้นคานๆ นี้จะมีค่า PARAMETER ที่เราทราบค่าอยู่ทั้งหมด 3 ค่า คือ
EQ.EQ + C = 3
และคานๆ นี้ก็จะมีค่า UNKOWN อยู่ทั้งหมด 3 ค่าด้วยกัน คือ
R (REACTIONS) = 3
ดังนั้นในเมื่อค่า PARAMETER ที่เรา ทราบค่า นั้นเท่ากันกับตัว UNKNOWN ที่ ไม่ทราบค่าเหมือนกันกับกรณีของคานรูปเมื่อวานเลยนะครับ ก็จะถือได้ว่าโครงสร้างๆ นี้เป็นโครงสร้างคานที่มีสภาพอย่างง่าย เราจึงสามารถที่จะทำการวิเคราะห์โครงสร้างได้ด้วยหลักการทางด้านสถิตศาสตร์ (STATICALLY DETERMINATE BEAM) และยังถือว่าคานๆ นี้มีเสถียรภาพ (STABLE) ต่อการรับ นน ที่ดีเพียงพออีกด้วย
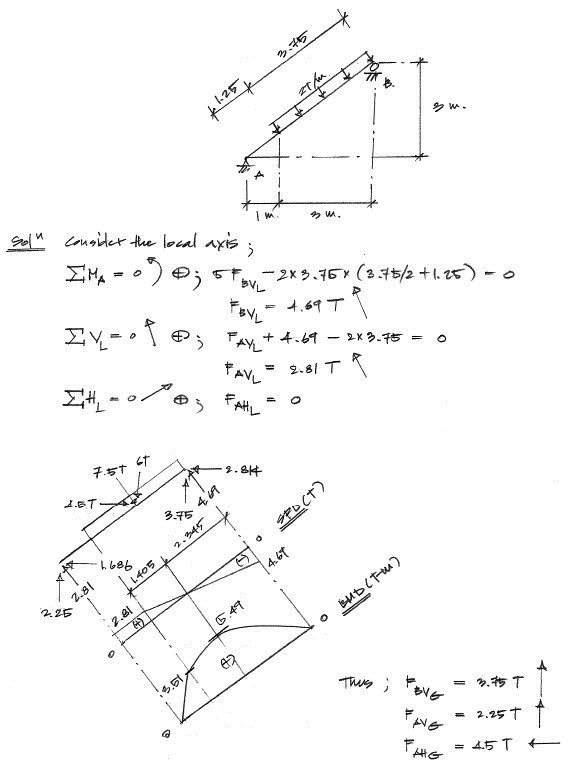
ดังนั้นการวิเคราะห์โครงสร้างคานดังรูปๆ นี้จะสามารถอาศัยสมการสมดุล (EQUILIBRIUM EQUATIONS) ทั้ง 3 ได้ คือ สมการสมดุลสำหรับโมเมนต์ (EQUILIBRIUM EQUATIONS OF MOMENTUM FORCES) สมการสมดุลสำหรับแรงกระทำในแนวดิ่ง (EQUILIBRIUM EQUATIONS OF VERTICAL FORCES) สมการสมดุลสำหรับแรงกระทำในแนวราบ (EQUILIBRIUM EQUATIONS OF HORIZONTAL FORCES) นะครับ
โดยหัวใจสำคัญในการวิเคราะห์โครงสร้างคานแบบนี้จะอยู่ที่การพิจารณาโครงสร้างภายในระนาบของส่วนโครงสร้างคานเอง (LOCAL AXIS) ซึ่งประเด็นนี้เองจะเป็นประเด็นที่มีความแตกต่างกันออกไปจากรูปคานในโพสต์ของเมื่อสองวันก่อนนะครับ ดังนั้นจะพบว่าค่าแรงปฏิกิริยาที่จุดรองรับต่างๆ นั้นจะไม่สามารถทำการคำนวณออกมาได้อย่างตรงไปตรงมาเหมือนกันกับในโพสต์ของเมื่อสองวันก่อนหน้านี้นะครับ
เราจะพบว่าค่าแรงปฏิกิริยาในแนวราบที่จุดรองรับ A ในข้อนี้จะมีค่าไม่เท่ากับ 0 ซึ่งจะเป็นข้อแตกต่างออกไปจากโพสต์ของเมื่อสองวันก่อนหน้านี้นะครับ สาเหตุนั้นเป็นเพราะว่าในโครงสร้างของเรานั้นจะประกอบไปด้วยแรงในแนวราบที่เกิดจากการแตกแรงของ นน บรรทุกที่กระทำบนระนาบเอียงของคานๆ นี้ และ หากดูแรงภายในของโครงสร้างนี้จะพบว่าในคานๆ นี้จะไม่มีแรงตามแนวแกนกระทำเลยเพราะว่าการแตกแรงของแรงปฏิกิริยา ณ จุดรองรับจะทำให้คานๆ นี้เกิดสภาวะสมดุลขึ้นในโครงสร้างๆ นี้ ซึ่งจะเป็นข้อแตกต่างกันออกไปจากรูปคานในโพสต์ของเมื่อสองวันก่อนหน้านี้นั่นเองนะครับ
สุดท้ายพอทำการวิเคราะห์หาค่าแรงปฏิกิริยา ณ จุดรองรับ และ หาค่าแรงภายในต่างๆ ได้หมดแล้ว ต่อไปเราก็จะสามารถนำค่าแรงข้างต้นเหล่านี้ไปทำการเขียนแผนภาพแรงเฉือน (SHEAR FORCE DIAGRAM) และแผนภาพแรงดัด (BENDING MOMENT DIAGRAM) ได้ในที่สุดครับ
จะสังเกตได้ว่าคานในรูปวันนี้นั้นจะมีความแตกต่างออกไปจากรูปคานเมื่อสองวันก่อนหน้านี้ นั่นเป็นเพราะว่ารูปแบบของ นน บรรทุกในรูปที่ 3 นี้เป็นเพียงรูปเดียวที่ทำให้คานนั้นเกิดแรงในแนวราบนั่นเองนะครับ
หวังว่าความรู้เล็กๆ น้อยๆ ที่ผมได้นำมาฝากแก่เพื่อนๆ ทุกๆ ท่านในวันนี้จะมีประโยชน์ต่อทุกๆ ท่านไม่มากก็น้อย และ จนกว่าจะพบกันใหม่นะครับ